How Often Does the Best Chess Player Win?

In this weeks installment of Matt solves a riddle with a simulation, we have the ridder express question from fivethirtyeight.  In a chess match, 12 games are played and the first player to 6.5 points wins.  You get 1 point for a win, 0.5 points for a draw, and 0 for a loss.  It’s very possible that the best player loses a chess match with this scoring system and only twelve games.  It’s more than football, baseball, or basketball, but is 12 games enough to decide?  Furthermore, how many games would be required to determine the winner 90% or 99% of the time.

How often does the best chess player win a 12 game match?

This first question is the easiest to answer (that’s probably why it came first).  We know that the player in question wins 20% of the time, loses 15% of the time, and ties 65% of the time.  Now, we just set up a monte carlo simulation for each match and run it a bunch of times. You can see my code in python below.  Instead of running the full 12 matches, I instead checked after each game to see if any player had more than the six points that would signify a victory and ended the match there.

import random

# Player odds
player1winOdds = .20
player1tieOdds = .65
player1loseOdds = .15

# Keep track of wins
player1wins = 0
player2wins = 0

# How many matches to simulate
numMatches = 10000000

# Iterates over the many matches
for i in range(numMatches):
	# Resets player points
	player1points = 0.0
	player2points = 0.0

	# Represents a match of several games
	while True:
		# Generates a random floating point number from 0-1
		x = random.random()

		# If the random number is less than the winning odds,
		#  then he won, if it's between the winning and tie odds,
		#  then a tie, and otherwise a loss
		if x < player1winOdds:
			player1points += 1
		elif x = 6.5:
			player1wins += 1
			break
		elif player2points >= 6.5:
			player2wins += 1
			break

# Print info
print str(numMatches) + " matches"
print "Player 1 won " + str(player1wins)
print player1wins * 100.0 / numMatches

After ten million simulated matches, the answer is that the best player wins about 67.9% of the time.  This is definitely lower than I expected and leads naturally to the next question.

How many games would be needed for the best player to win 75%, 90%, or 99% of the time?

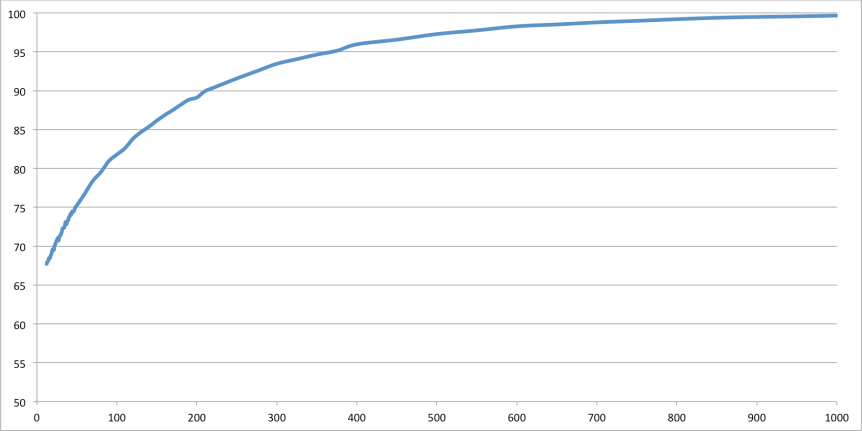
This question, while pretty simple does complicate the simulation.  Instead of just simulating a bunch of matches, we need to simulate them for a bunch of different number of games.  Now, it would be possible to automatically simulate these as the number of games is varied and spit out a single answer.  But instead, I chose to just run the simulation for each and then print out the number and plot them. If you look at the chart below, you can see that the answers are: 49 matches for 75%, 220 matches for 90%, and 800 matches for 99% (roughly).

You can choose your range by manually trying numbers or by plotting every number and looking at if afterward.  I initially tried a few numbers and then after I found the answer put in the ranges below to show exactly what I wanted while saving time.  I tested every game up to the 75% answer, then every 10 games up to 90% then every 25 up to 95%, then every 50 up to 1000.

import random

# Player odds
player1winOdds = .20
player1tieOdds = .65
player1loseOdds = .15

# The number of matches to simulate for each test with
#  a certain number of games in it
numMatches = 100000

# Testing ranges for number of games in a match
numList = []
numList.extend(range(12,50, 1))
numList.extend(range(50,220, 10))
numList.extend(range(250,400, 25))
numList.extend(range(400,1001, 50))

# Iterates through the list of the number of games to use
#  Previously was "for k in range(12,1000):"
for k in numList:
	# Reset and keep track of wins
	player1wins = 0
	player2wins = 0

	# Iterates over the many matches
	for i in range(numMatches):
		# Resets player points
		player1points = 0.0
		player2points = 0.0

		# Represents a match of several games
		while True:
			# Generates a random floating point number from 0-1
			x = random.random()

			# If the random number is less than the winning odds,
			#  then he won, if it's between the winning and tie odds,
			#  then a tie, and otherwise a loss
			if x < player1winOdds:
				player1points += 1
			elif x  k/2.0:
				player1wins += 1
				break
			elif player2points > k/2.0:
				player2wins += 1
				break

	# Print info (num games, win percentage)
	print str(k) + ", " + str(player1wins *100.0 / numMatches)

asdfasd